はじめに
こんにちは、橋渡と申します。
今回のブログではProphetを用いて、時系列データから将来の予測を行うための一連のプロセスについて書きたいと思います。
全体の流れ
1.Prophetとは
2.実施すること
3.ライブラリのインポート
4.サンプルデータの生成
5.データの分割と学習
6.予測
7.評価指標の算出
1. Prophetとは
Prophetは、Facebook(現Meta)が開発した時系列予測のためのオープンソースです。ビジネスやデータ分析の現場でよく使われており、PythonやRで利用できます。
時系列予測とは、過去のデータをもとに将来の値を予測することです。例えば、売上の推移などを予測するのに役立ちます。
2. 実施すること
このブログではProphetについてのみでなく、時系列データに基づいて予測を行うための一連のプロセスを紹介します。主に以下のステップを実施します:
-
データの準備
予測モデルに適したデータを準備します。Prophetでは、ds(日付)とy(予測値)という2つのカラムが必要です。今回はサンプルデータを生成します。 -
データの分割
予測モデル構築のため、データを訓練データとテストデータに分割します。時系列データであることから時系列に沿った分割を行います。この分割により、モデルの性能を客観的に評価できます。 -
モデルの学習
分割した訓練データを使って、Prophetモデルを学習させます。 -
予測
訓練データを使って学習させたモデルを用いて、将来の予測を行います。これにより、将来の特定の期間における予測値を得ることができます。 -
予測結果の可視化
予測結果を視覚的に確認するため、グラフを生成します。可視化することで予測が実際のデータにどれほど合っているのかを直感的に理解することができます。 -
評価指標の算出
最後に、予測の精度を評価するために、MAPE, WAPE, MAE, RMSEを指標としてモデルの性能を評価します。
この一連の流れに沿って、Prophetを使った時系列予測の実装方法を解説していきます。
3. ライブラリのインポート
!pip install japanize-matplotlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from prophet import Prophet
from sklearn.metrics import mean_absolute_error, mean_squared_error4. サンプルデータの生成
日付ごとに「上昇傾向にあるトレンド」「季節ごとの変動」「ランダムなノイズ」の3つの要素を組み合わせた時系列データを生成し、可視化します。
# パラメータ設定
np.random.seed(42)
start_date = pd.to_datetime("2022-01-01")
end_date = pd.to_datetime("2025-03-31")
date_range = pd.date_range(start=start_date, end=end_date, freq="D")
# データ生成
trend = np.linspace(30, 200, len(date_range))
seasonality = 15 * np.sin(2 * np.pi * 5 * date_range.dayofyear / 365.25)
noise = np.random.normal(0, 1, len(date_range))
data = trend + seasonality + noise
df = pd.DataFrame({'ds': date_range, 'y': data})
df["ds"] = pd.to_datetime(df["ds"])
# 生成したデータの可視化
plt.figure(figsize=(12, 4))
sns.lineplot(data=df, x="ds", y="y", color="gray", alpha=0.7)
sns.despine()
plt.title("生成したサンプルデータ(期間:2022/01/01~2025/03/31)", fontsize=12)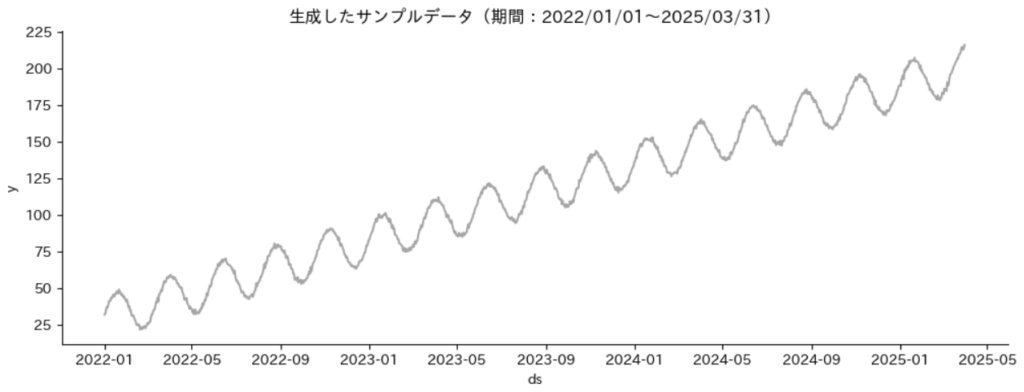
5. データの分割と学習
以下のとおりデータを分割し、シンプルなProphetのモデルを定義し学習します。
訓練データ:2022/01/01~2024/12/31
テストデータ:2025/01/01~2025/03/31
# データ分割
split_date = "2024-12-31"
train = df[df["ds"] <= split_date]
test = df[df["ds"] > split_date]
# モデルのインスタンス化
model = Prophet()
# 学習
model.fit(train)6. 予測
Prophetの学習済モデルからの予測結果を可視化します。
ノイズまで捉えるのは難しいですが、非常に精度良く予測できていることが確認できます。
# テストデータを用いて予測
forecast = model.predict(test)
# 予測結果を可視化
plt.figure(figsize=(12, 4))
# 実測値
plt.plot(test["ds"], test["y"], color="gray", label="実測値", alpha=0.5)
# 予測値
plt.plot(forecast["ds"], forecast["yhat"], color="red", label="予測値", alpha=0.5)
sns.despine()
plt.legend()
plt.title("Prophetによる予測結果")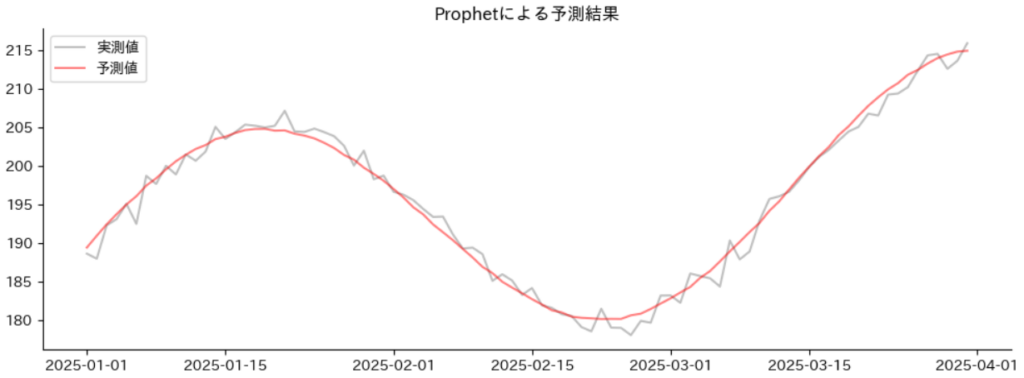
将来の期間を作成して予測することも可能です。
# 予測する将来の期間を生成する
# 2025-03-31まで作成
future = model.make_future_dataframe(periods=90)
print(f"開始日: {future['ds'].min().strftime('%Y-%m-%d')}, 終了日:{future['ds'].max().strftime('%Y-%m-%d')}")
future.tail()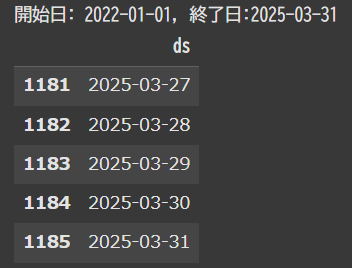
Prophetの学習結果と予測を可視化します。
青が実測値、赤がProphetの予測値です。
2025/01/01以降はテスト期間ですので、Prophetの予測値のみが表示されています。
Prophetの予測値が、ほぼ実測値に重なっていることから適切に学習していることが確認できます。
# 予測
forecast = model.predict(future)
plt.figure(figsize=(12, 4))
# 実測値
plt.plot(train["ds"], train["y"], color="blue", label="実測値")
# Prophetの学習結果と予測
plt.plot(forecast["ds"], forecast["yhat"], color="red", label="予測値")
sns.despine()
plt.legend()
plt.title("Prophetの学習結果と予測")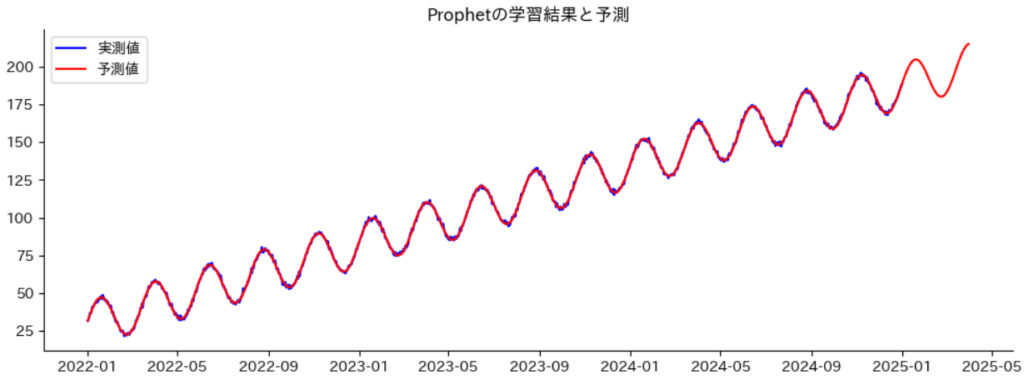
さらにProphetは、予測結果をわかりやすく分解してくれるのが特徴です。具体的には、以下の3つの主要な要素に分けて、どのように予測が形成されたのかを視覚的に理解できます。
-
トレンド
長期的な傾向を表し、データの全体的な方向性を把握できます。 -
季節性
一定の周期で繰り返すパターンを示します。月ごとや曜日ごとの変動や、年間を通じた変動を確認できます。 -
イベントや休日効果
特定のイベントや祝日、プロモーションなどがデータに与える影響を考慮します。
必要に応じて外部要因(天気など)を追加することも可能です。これにより、天候が売上に与える影響なども予測に反映できます。
今回はイベントや外部要因(天気)はモデルに含めていないので表示されませんが、以下のように分解して可視化することができます。
長期的に上昇するトレンドと季節性を考慮したデータを生成し学習させましたが、Prophetはそれらを適切に学習し、分解していることがわかります。
fig = model.plot_components(forecast)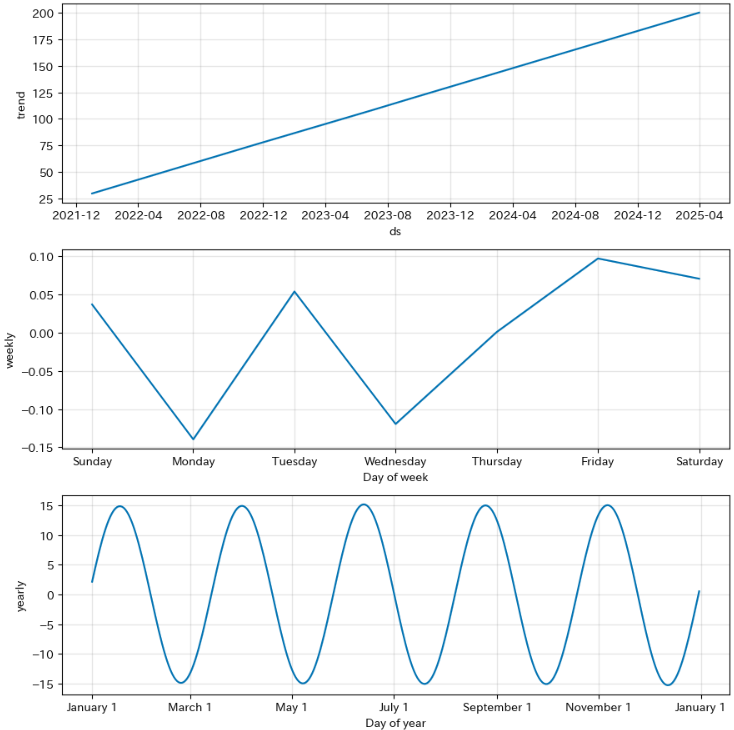
予測結果を格納したforecastには上記で説明した要素ごとの値が格納されています。
forecastの一部分を表示します。
print(f"forecastの形状: {forecast.shape}")
forecast.iloc[:3, :5]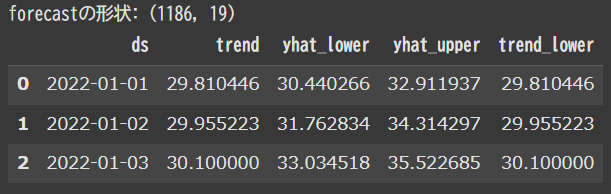
7. 評価指標の算出
精度の評価には以下の4つを使用します。
- Mean Absolute Percentage Error (MAPE)
MAPEは、予測値と実際の値の絶対誤差をパーセンテージで示す指標です。予測精度がどれくらい良いかを、誤差の割合で直感的に理解できます。 - Weighted Absolute Percentage Error (WAPE)
WAPEは、各データポイントの絶対誤差の合計を、実測値の合計で割ることによって得られます。 - Mean Absolute Error (MAE)
MAEは、予測値と実際の値の絶対誤差の平均を取る指標です。誤差が大きすぎないか、予測の精度がどれくらい良いかを評価できます。MAEは単純で理解しやすい指標ですが、大きな誤差に対しては敏感ではありません。 - Root Mean Squared Error (RMSE)
RMSEは、二乗誤差の平均の平方根を取ることで、大きな誤差に対して特に敏感な指標となります。RMSEは、大きな誤差が発生した場合にその影響が強調されるため、誤差の大きさに敏感です。
今回は規則性があり、ノイズも少ないデータを生成し使用したことから、MAPEが0.52であるなど、非常に精度が良いことが確認できます。
実際のデータは複雑であり、Prophetの学習について試行錯誤する必要があります。
# 評価指標を算出するクラスを定義
class ShowMetrics(object):
def mape(self, y_true, y_pred):
"""Mean Absolute Percentage Error (MAPE)
Args:
y_true(numpy array or list): 実測値
y_pred(numpy array or list): 予測値
Return:
MAPE value (float)
"""
y_true, y_pred = np.array(y_true), np.array(y_pred)
mask = y_true != 0 # 実測値が0の場合を除外する
return np.mean(np.abs((y_true[mask] - y_pred[mask]) / y_true[mask])) * 100
def wape(self, y_true, y_pred):
"""Weighted Absolute Percentage Error (WAPE)
Args:
y_true(numpy array or list): 実測値
y_pred(numpy array or list): 予測値
Return:
WAPE value (float)
"""
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.sum(np.abs(y_true - y_pred)) / np.sum(y_true) * 100
def get_metrics(self, y_true, y_pred):
"""MAPE, WAPE, MAE, RMSEを表示する関数
Args:
y_true(numpy array or list): 実測値
y_pred(numpy array or list): 予測値
"""
mape_value = self.mape(y_true, y_pred)
wape_value = self.wape(y_true, y_pred)
mae = mean_absolute_error(y_true, y_pred)
rmse = np.sqrt(mean_squared_error(y_true, y_pred))
print(f"MAPE: {mape_value}")
print(f"WAPE: {wape_value}")
print(f"MAE: {mae}")
print(f"RMSE: {rmse}")
# 実測値・予測値を格納
y_true = test["y"].values
y_pred = forecast[forecast["ds"] > split_date]["yhat"].values
# インスタンス化
metrics = ShowMetrics()
# 評価指標を算出
metrics.get_metrics(y_true, y_pred)
終わりに
今回は、時系列予測ツールである Prophet を用いて、シンプルな時系列データの予測を行いました。Prophetは、トレンドや季節性の変動を捉え、視覚的にもわかりやすい予測結果を確認することができるため、分析に非常に適しています。
本記事では、特にイベントや外部要因を考慮せず、基本的なトレンドと季節性に基づいた予測を行いましたが、Prophetはさまざまな機能を備えています。特定の祝日やイベント、天候といった外部要因をモデルに組み込むことで、より精度の高い予測を実現できます。
ぜひ、Prophetを皆さんの分析にも役立ててみてください。
