はじめに

こんにちは、橋渡と申します。
今回は、PyTorchを用いて機械学習の学習がどのように行われるかを観察したいと思います。
PyTorchはPythonのオープンソースの機械学習ライブラリであり、主にディープラーニングで使用されますが、
学習アルゴリズムを理解する上でも非常にわかりやすいフレームワークです。

全体の流れ

1.実施すること
2.ライブラリのインポート
3.サンプルデータの生成
4.生成データの可視化
5.モデルの定義
6.学習
7.学習過程の可視化

1.実施すること

・PyTorchを用いて線形単回帰モデルを定義します。
・学習過程で重み（傾き・切片）がどのように最適化されるのか観察します。
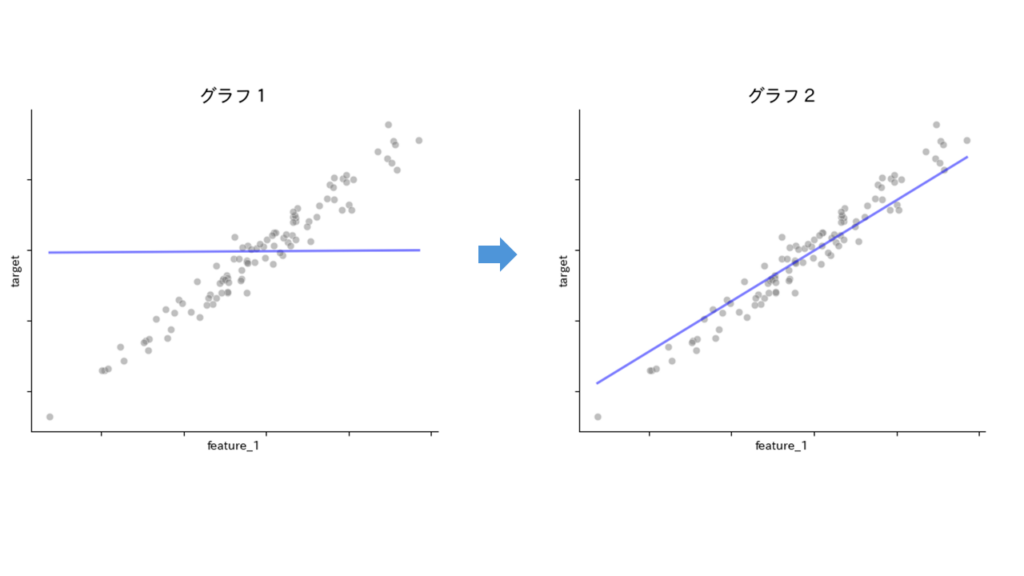
・最終的にグラフ１からグラフ２のように重み（傾き・切片）が最適化される過程を可視化したいと思います。

2.ライブラリのインポート

使用するライブラリをインポートします。

!pip install japanize-matplotlib

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
import torch
import torch.nn as nn
from sklearn.datasets import make_regression

3.サンプルデータの生成

特徴量（説明変数）を１種類として架空のサンプルデータを100個生成します。
作成したデータは表形式で保持し、５件表示してみます。

# サンプルデータ生成
# X に特徴量（説明変数）、 y に目的変数が格納される 
X, y = make_regression(
    n_samples=100,  # サンプル数
    n_features=1,   # 特徴量数
    noise=10,       # ノイズ
    random_state=42 # シードを固定
)

# 表形式に変更
df = pd.DataFrame(np.hstack([X, y.reshape(-1, 1)]), columns=["feature_1", "target"])
print(f"サンプル数: {len(df)}")
display(df.head())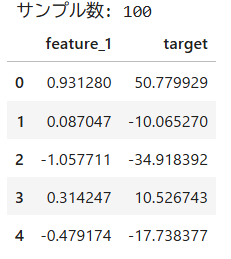

4.生成データの可視化

下記のとおり正の相関があるデータとなっており、今回はfeature_1からtargetを予測する直線を考えます。

plt.figure(figsize=(6, 4))
sns.scatterplot(data=df, x="feature_1", y="target", color="gray", alpha=0.7)
sns.despine()
plt.title("散布図（正の相関）")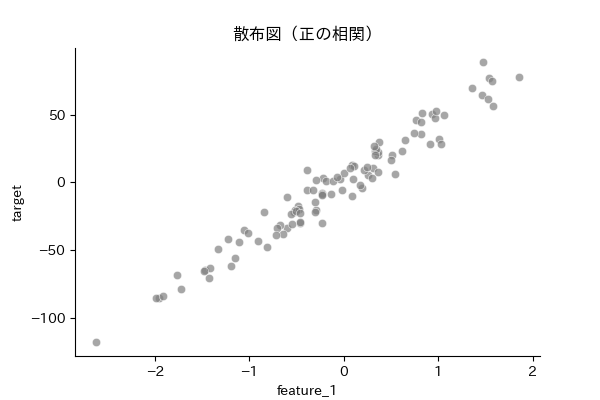

5.モデルの定義

ではfeature_1からtargetを予測する直線として、線形単回帰のモデルを定義します。
線形単回帰モデルとは、1つの特徴量をもとに目的変数を予測するための方法です。
y = ax + bという１次関数 をイメージいただけるといいと思います。
この場合x:feature_1、y:target、a:傾き、b:切片となり、最適なaとbを求めるということを行います。

# 線形単回帰モデルを定義するクラス
class SimpleLinearRegression(nn.Module):
    def __init__(self, in_features=1, out_features=1):
        super().__init__()
        # 全結合層を定義
        # 入力の特徴量数 in_features と出力数 out_features を指定
        self.linear = nn.Linear(in_features, out_features)

    def forward(self, x):
        # 順伝播を定義
        # 入力 x に対して線形変換を適用し、出力 out を生成
        out = self.linear(x)
        return out

# モデルのインスタンス化
# SimpleLinearRegression() で線形単回帰モデルを作成
# y = ax + bのイメージ
model = SimpleLinearRegression()

# 損失関数を平均二乗誤差（MSE）に設定
# 予測と実際の値の差を二乗して平均した値を損失として使用
criterion = nn.MSELoss()

# 最適化手法に確率的勾配降下法(SGD)を使用
# lr=0.01 は学習率、学習の進行具合を設定
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

6.学習

学習の流れは、以下のとおりです。
1.特徴量をモデルに入力
2.モデルが予測値を出力
3.予測値と実際の値の誤差を計算
4.勾配の計算（どの方向に重み（傾き・切片）を調整すれば誤差が減るかの方向性）
5.重み（傾き・切片）の値を更新（勾配を使って少しずつ調整）

初回とそれ以降は10回の学習ごとに重み（傾き・切片）を記録します。

# モデル入力用に学習データを変換
X_train = torch.tensor(df["feature_1"].values, dtype=torch.float32).view(-1, 1)
y_train = torch.tensor(df["target"].values, dtype=torch.float32).view(-1, 1)

# 重み(傾き)、バイアス(切片)、損失(誤差)を記録するリストを初期化
weights = []        # 重み(傾き)を格納するリスト
biases = []         # バイアス(切片)を格納するリスト
train_losses = []   # loss(損失)を格納するリスト

# 学習回数（エポック数）を110回に設定
# 最終的に描画するグラフ数の観点から110回としている
num_epochs = 110

# エポック数のループ（学習を110回行う）
for epoch in range(1, num_epochs+1, 1):

    # 勾配をリセット
    optimizer.zero_grad()

    # モデルに特徴量を入力し、予測値を出力
    predictions = model(X_train)

    # 予測値と実際の値との損失（誤差）を計算
    loss = criterion(predictions, y_train)

    # 損失に基づいて勾配の計算
    loss.backward()

    # 勾配を使って重み（傾き・切片）を更新
    optimizer.step()

    # 初回と学習回数10回ごとに重みなどを記録する
    if epoch == 1 or epoch % 10 == 0:
        weights.append(model.linear.weight.detach().numpy().item()) # 重み（傾き）の値を保存
        biases.append(model.linear.bias.detach().numpy().item())    # バイアス（切片）の値を保存
        train_losses.append(np.sqrt(loss.detach().numpy()))         # 損失を保存（RMSE）

7.学習過程の可視化

記録した重み（傾き・切片）を学習データ上に可視化します。
下記のグラフを見ていくと、学習１回目ではまったくデータに適合していませんでしたが、学習を重ねるについて誤差が少なくなりデータに当てはまっていく様子が見えると思います。
このモデルの重み（傾き・切片）が適切に調整（最適化）されていく過程を学習というのですね。
110回目の学習でも、まだあと少し調整されそうですが、この学習回数なども試行錯誤ですね。

# グラフ描画用の配列を準備
def calc_y(weight, bias, x):
    # 線形関係 y = ax + b の式を使って、yの値を計算
    y = bias + weight * x  
    return y

plot_x = np.linspace(X.min(), X.max(), num=50)

# plot_y には、各エポックごとの重みとバイアスを使って計算されたyの値を格納
plot_y = []
# weights と biases は、学習中に記録された重みとバイアスのリスト
# zip(weights, biases) で重みとバイアスをペアにして反復処理
for weight, bias in zip(weights, biases):
    # calc_y 関数を使って、各重みとバイアスに対応する予測値yを計算
    plot_y.append(calc_y(weight, bias, plot_x))

# グラフの描画用に4行3列のサブプロットを作成（全体で12個のグラフ）
fig, axes = plt.subplots(nrows=4, ncols=3, figsize=(15, 15))
axes = axes.ravel()

# plot_y の長さ（重みとバイアスが記録された回数分）に合わせてループ
for i in range(len(plot_y)):
    # 学習データの散布図を描画
    sns.scatterplot(data=df, x="feature_1", y="target", color="gray", alpha=0.5, ax=axes[i])
    # plot_y[i] には学習回数ごとの回帰直線のy値が格納されている
    axes[i].plot(plot_x, plot_y[i], color="blue", alpha=0.5, linewidth=2)
    # 軸の枠線を除去（見た目をシンプルにする）
    sns.despine(ax=axes[i])
    axes[i].set_title(f"学習回数：{i*10 if i > 0 else 1}回目", fontsize=15)
    # x軸とy軸のラベルを非表示
    axes[i].set_xlabel('')
    axes[i].set_ylabel('')
    # 目盛りラベルを非表示
    axes[i].tick_params(axis='x', labelbottom=False)
    axes[i].tick_params(axis='y', labelleft=False)

plt.tight_layout()
plt.show()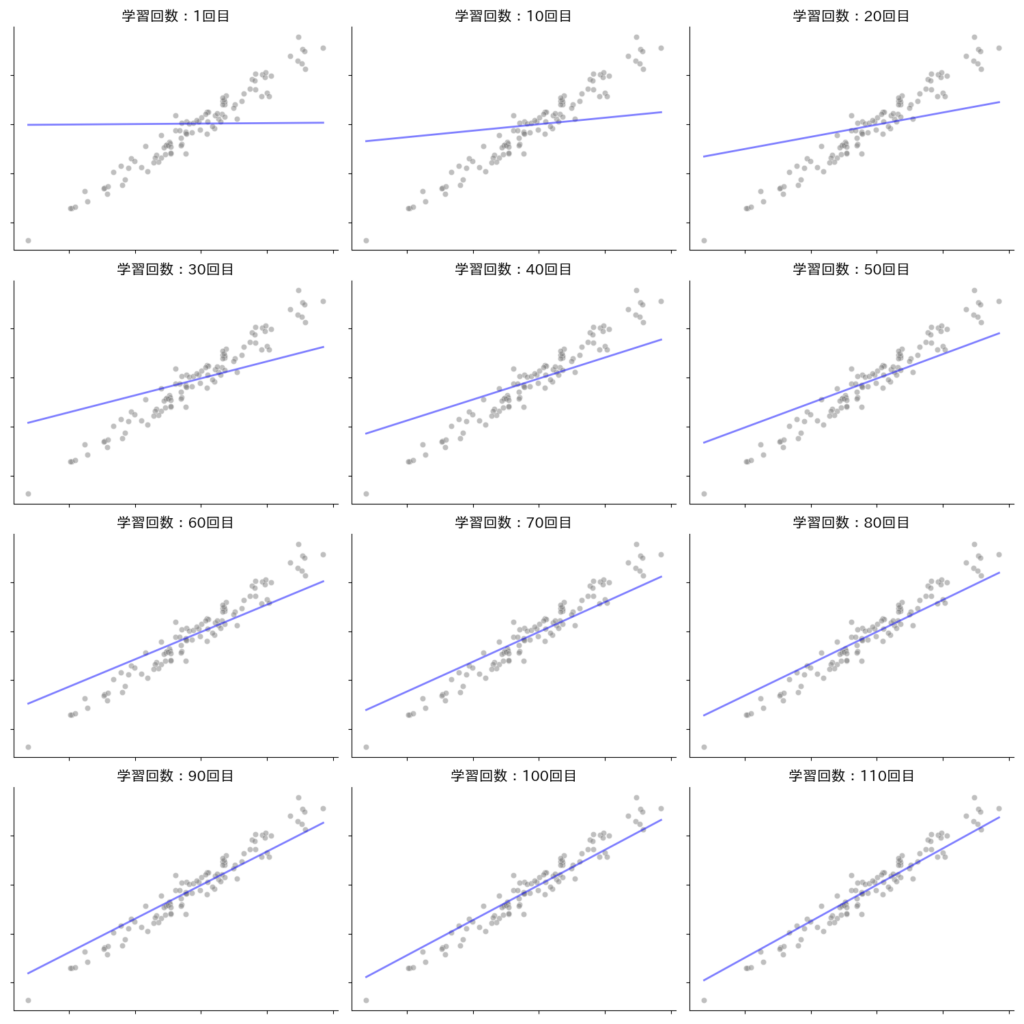

終わりに

今回はPyTorchを用いて機械学習の学習過程を観察しました。
学習にフォーカスして書かせていただきましたが、このほかにもデータの前処理、学習データの分割方法、損失関数、データの学習単位などさまざまな観点があります。
また記事をかけるように頑張りたいと思います。
最後までご覧いただき、ありがとうございました。