はじめに
- 分類タスク(2値分類モデル)の評価指標の基本AUCについて書く
- 本記事ではAUCをみてどう評価するかではなく算出過程をメインに説明する
- ROC曲線がどのように描かれるかイメージがつかない方にとって少しでも有益になると嬉しい
AUCとROC曲線の概要
- AUCとはArea Under the Curveの略
- ROC曲線を描いた際の曲線の下部の面積のこと
- 曲線の下の面積→Area Under the Curve
- AUCの取りうる範囲は0~1
- 1は予測精度が最大であることを示す
- 0.5は当てずっぽうモデルであることを示す(コイントスして判別しているのと同じかも)
- 0も予測精度が最大であることを示す。ただし陽性陰性を逆転させて予測してしまっている
- ROC曲線とは縦軸にTrue Positive Rate、横軸にFalse Positive Rateをとり閾値(threshold)を1→0に動かしたときにとる軌跡をプロットしたもの
- 左下はTPRもFPRもゼロの地点
- ここから閾値を動かしつつ率の変動をプロットしていく
- 真の値が陽性であるデータを正しく陽性判定できているなら上に移動
- →TPRが上昇
- 真の値が陰性であるデータを誤って陽性判定してしまうと右に移動
- →FPRが上昇
AUCとROC曲線の理解が深まる数式
True Positive Rate(TPR)
※Sensitivity(感度)とも呼ぶ
- TP:True Positive(真陽性)の数
- FN:False Negative(偽陰性)の数 ※真の値はPositive
→つまりTPRとは真の値が陽性であるデータのうち、モデルが正しく陽性と予測できた割合のこと
False Positive Rate(FPR)
※1 - Specificity(1 - 特異度)とも呼ぶ
- FP: False Positive(偽陽性)の数 ※真の値はNegative
- TN: True Negative(真陰性)の数
→つまりFPRとは真の値が陰性であるデータのうち、モデルが誤って陽性と予測した割合のこと
数式の補足
- TP(True Positive):真の値が陽性で、モデルも陽性と予測したケース
- FP(False Positive):真の値が陰性で、モデルは陽性と予測したケース
- TN(True Negative):真の値が陰性で、モデルも陰性と予測したケース
- FN(False Negative):真の値が陽性で、モデルは陰性と予測したケース
AUCとROC曲線の例示
ある2値分類モデルに特徴量を与え推論させた結果の以下テーブルがあるとする
| データ | 正解ラベル | 予測確率 |
|---|---|---|
| y1 | 0 | 0.1 |
| y2 | 1 | 0.2 |
| y3 | 0 | 0.3 |
| y4 | 1 | 0.4 |
| y5 | 0 | 0.5 |
| y6 | 0 | 0.6 |
| y7 | 1 | 0.7 |
| y8 | 1 | 0.8 |
| y9 | 1 | 0.9 |
| y10 | 1 | 0.99 |
まず結論としてこのモデルのAUCは0.79となる
つづいてなぜそうなるのかだが、まずはAUCの算出する過程であるROCカーブを引いてみる
ROCカーブの引き方はつぎのとおり
- 予測確率の降順でデータを並び替える
- 前ステップの並び順のまま2値分類の真の値を走査していき
- 1(陽性)の場合上へ移動
- 0(陰性)の場合右へ移動
- とし、これを最後のデータまで繰り返す
- この結果描かれる曲線がROCカーブ
- データ数が少ないとガタガタしているが、データ数が1万くらいのケースを想像していただければなんとなく曲線になるのだろうなと思っていただけるはず
そしてこの曲線より下側の面積を計算すればAUCが算出されるという手順になっている
→今回はAUC=0.79となる
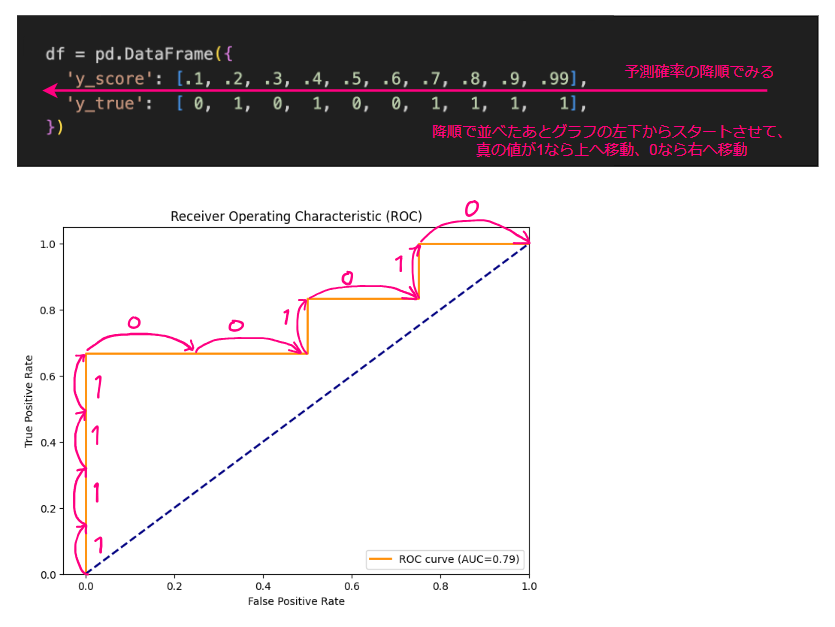
続いて、なぜ降順に並べ1、0をみてルールに即して動かしていくだけで描けるのか詳しく説明する
閾値を1→0と動かしていく中で描かれる軌跡がROCであり、まず初めに閾値1のケースから考える
ROCの定義から閾値1であれば予測確率1以下すべてを陰性と判定する場合になる
つまりすべて陰性判定することになるので
- 真の値が陽性のデータのうち正しく陽性と判別できているものはゼロ ∵すべて陰性と判定するためすべて不正解
- 真の値が陰性のデータのうち誤って陽性と判別してしまっているものゼロ ∵すべて陰性と判定するためすべて正解
したがって閾値1の場合、TPR=0%、FPR=0%となり一番左下に点をプロットする
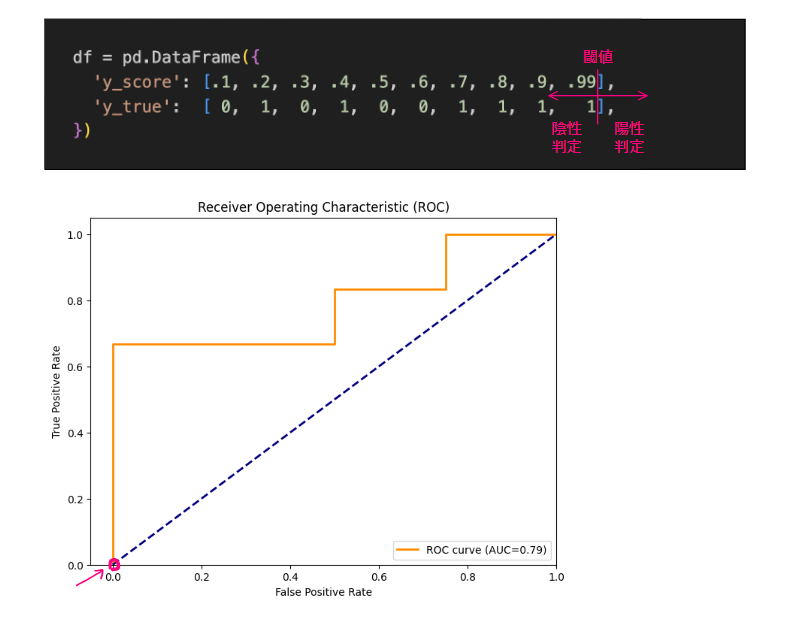
引き続き閾値を1→0と動かしていく。
閾値<0.99の時点で予測確率<0.99をすべてを陰性と判定する場合になる(数学的に厳密ではなさそうですがイメージで・・・)
つまり1つだけ正しく陽性判定し、ほかすべてを強制的に陰性判定することになるので
- 真の値が陽性のデータのうち正しく陽性と判別できているものは1つ→1/6
- 真の値が陰性のデータのうち誤って陽性と判別してしまっているものゼロ ∵真の値が陰性のものはすべて陰性と判定できているためすべて正解
したがって閾値1の場合、TPR?16.7%、FPR=0%となり少し上に点をプロットする
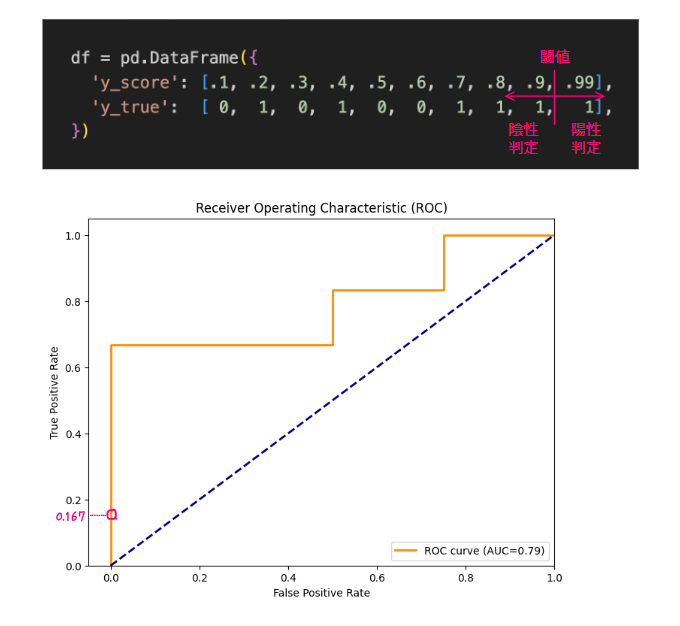
引き続き閾値を1→0と動かしていく。
閾値<0.6時点で予測確率<0.6をすべてを陰性と判定し、他方予測確率>=0.6は陽性と判定することになり、このタイミングで初めて真の値が陰性であるものを誤って陽性判定してしまうものが1つ発生することになる
つまり
- 真の値が陽性のデータのうち正しく陽性と判別できているものは4つ→4/6
- 真の値が陰性のデータのうち誤って陽性と判別してしまっているものは1つ→1/4
したがって閾値<0.6の場合、TPR?66.7%、FPR=25%となり初めて右に少し移動した点をプロットすることになる
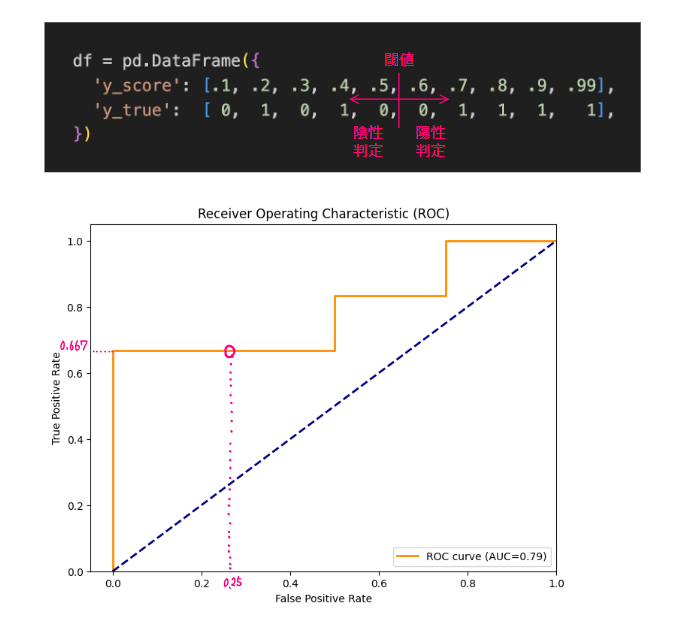
あとはこの操作を最後のデータまで続け軌跡を結ぶんだものがROCカーブとなる
したがって降順で並べ(閾値を1→0と動かしていくなかで)真の値を確認することを考えると
- 最初はすべて陰性判定するので陽性を陽性判定できるものはなくTPRゼロ、陰性を誤って陽性判定してしまうものもなくFPRもゼロ(=グラフ上、最も左下にプロットされる)
- 閾値を動かし真の値が1であるデータのラインを超えると、陽性判定することに切り替わるのでTPRが上昇(=上に移動)する
- 閾値を動かしつづけさらに真の値が1であるデータのラインを超えると、同じく陽性判定することに切り替わるのでさらにTPRが上昇(=上に移動)する
- つづいて閾値を動かしつづけさらに真の値が0であるデータのラインを超えると、今度は陽性と誤判定することに切り替わるのでFPRが上昇(=右に移動)する
- 最後まで繰り返せばROCカーブが描ける(※厳密にはTPRとFPRの値の計算はしなければならない)
結局このような操作を繰り返せば描けるため、決まりに沿って眺めるだけでROCカーブが描けるということになる
